Ctrlk
For the complete documentation index, see llms.txt. This page is also available as Markdown.

2.1 電腦世界的語言 ： 1 跟 0 的機器語言

電腦只有兩根手指頭？

　　據說，因為我們有十根手指頭，所以我們的世界中有「0、1、2、3、4、5、6、7、8、9」十個數字，也就是採用十進位。如果你相信這樣的說法，那你大可以想像電腦只有兩根手指頭，因為電腦世界中只有「1」跟「0」這兩個數字，而它用這兩個數字來儲存及表示訊息。

補充：
假如有一條電流通過的電路，信號可能是開或關，
我們也可以表示為是或否、對或錯、1或0，或其他兩個狀態的選項。
而單條電路上的開或關狀態，被稱為1個bit，
bit是計算機可以儲存的最小單位。

但當我們要表達複雜的訊息，我們將會有更多的電路（也就是更多bit及1和0），該怎麼表示呢？這時候你就該認識「二進位制」！

二進位制

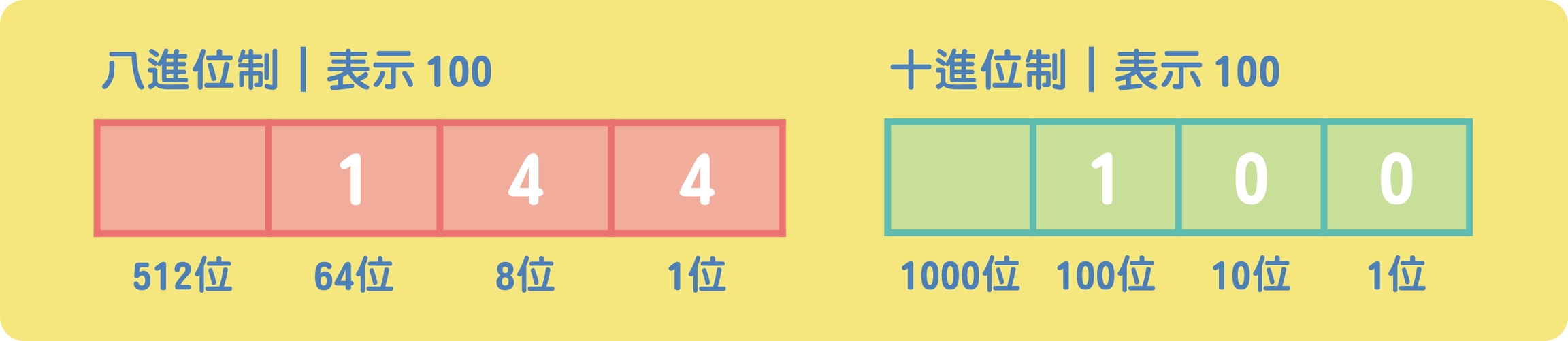
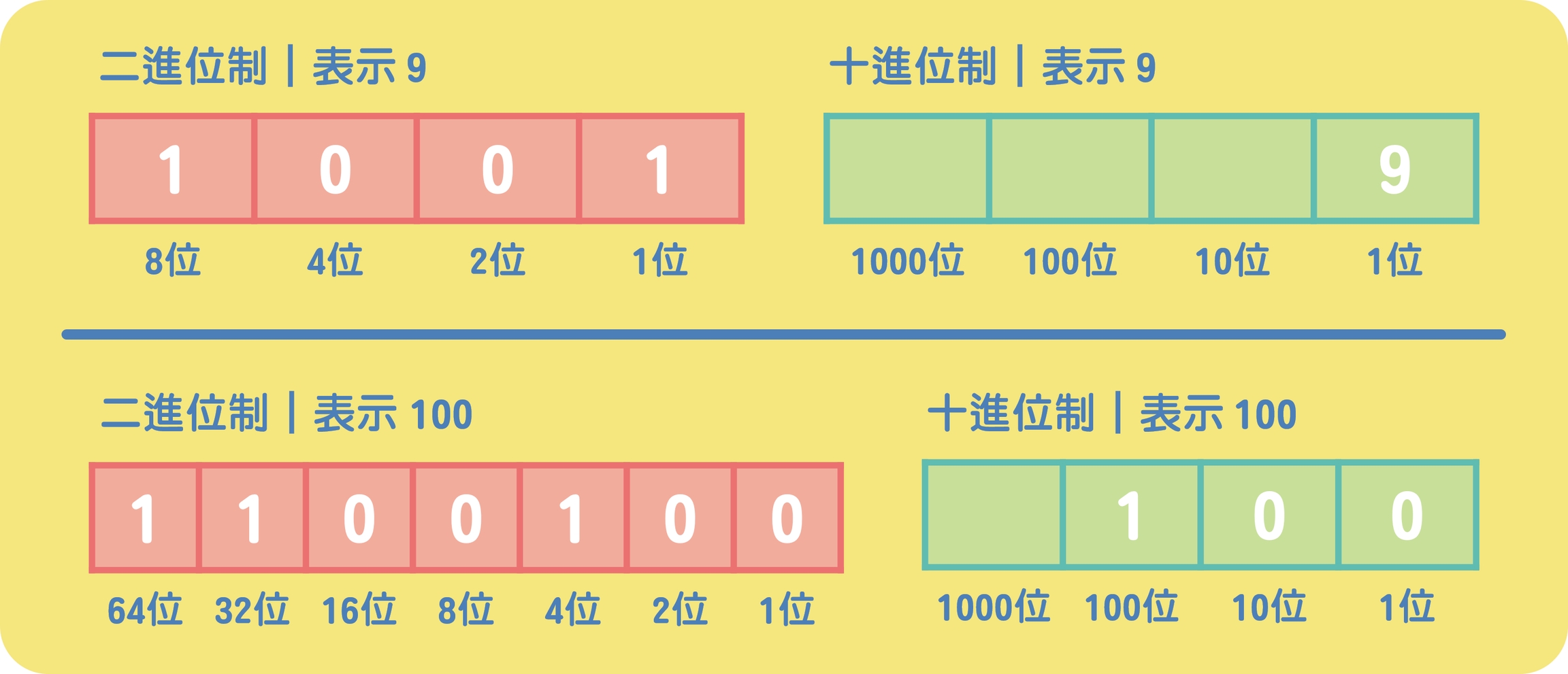
　　我們常用的十進位制，每進一位就是多乘10（如：個位、百位、千位 ···）。而二進位制顧名思義就是「逢2進位」，每進一位時，就是多乘2（如：1、2、4、8 ···）。

八進位制

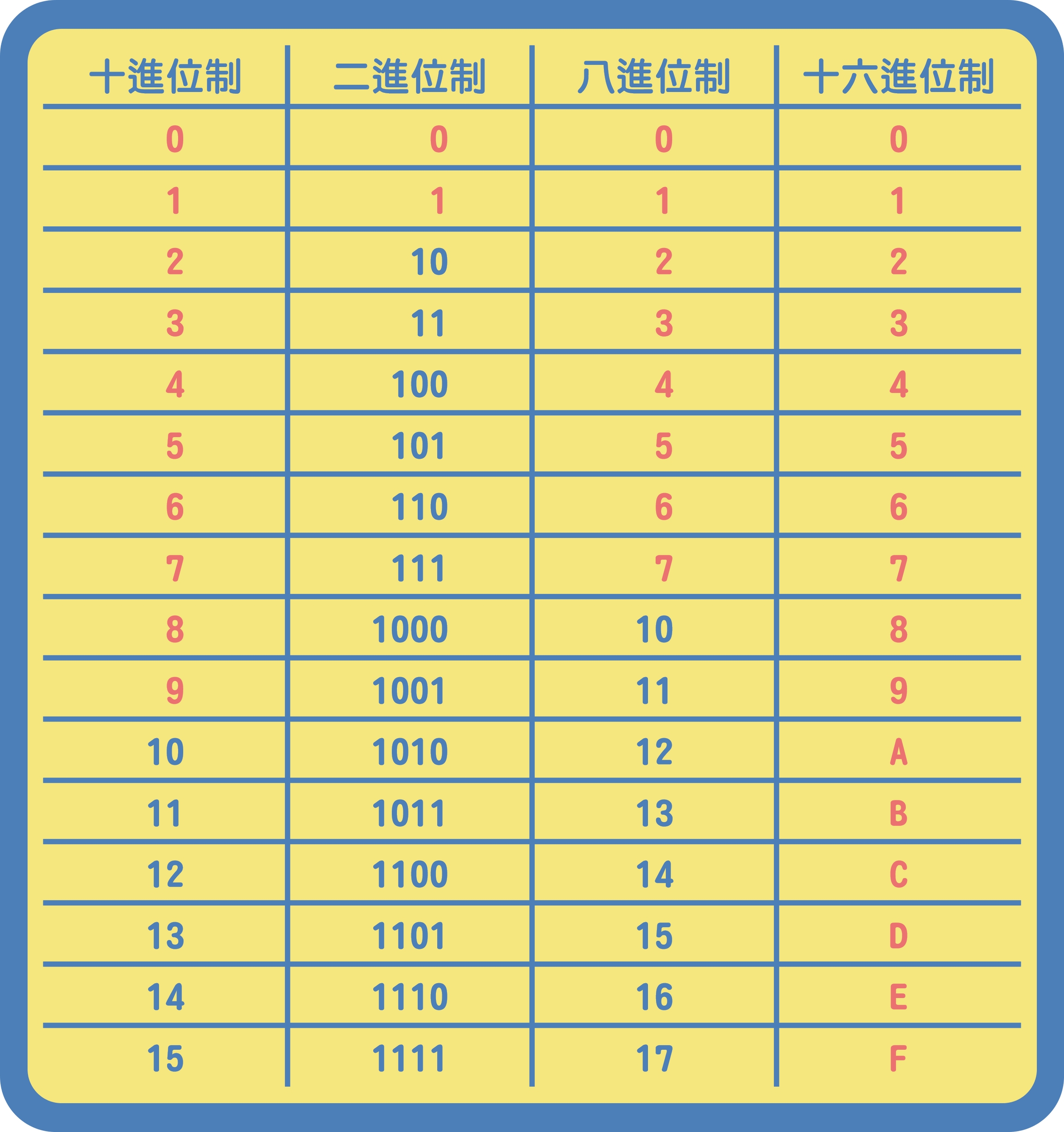
　　八進位制和二進位制雷同，數字符號為「0、1、2、3、4、5、6、7」，是「逢8進位」的。

十六進位制

　　講到十六進位制，你一定馬上就知道是「逢16進位」，沒錯！但十六進位制的數字符號可是有英文字母混入其中的喔！十六進位制的數字符號為「0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F」。

進位制轉換規則

　　在寫程式時不免需要轉換進位制，接下來就讓我們以圖解來看看較常見的十進位制轉換規則吧！

十進位制轉換為其他進位制

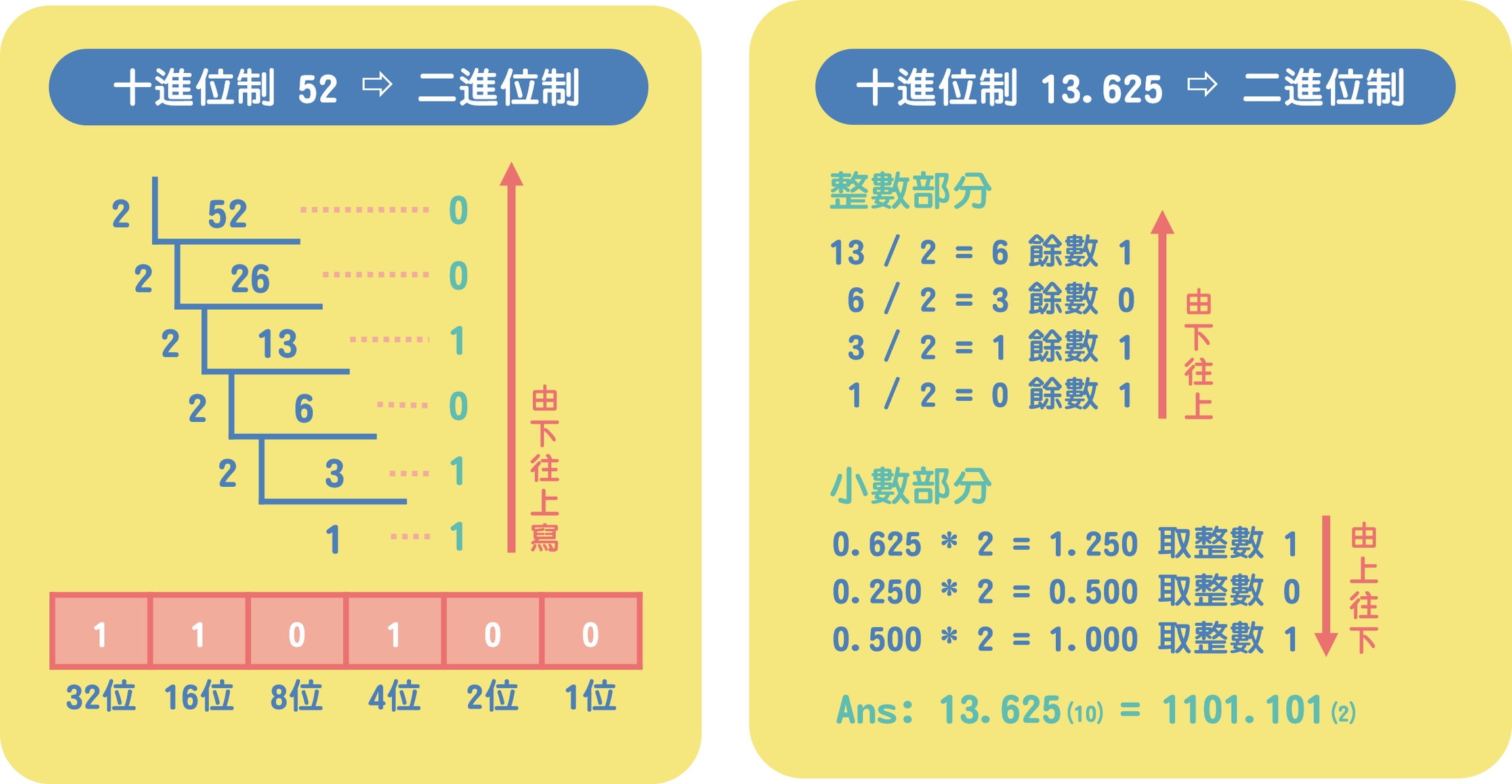
  • 整數（除法）：將【十進位「整數」/「欲轉換進位數」】，一直除到商數為 0，再依序「由下往上」取出餘數。

  • 小數 （乘法）： 將【十進位「小數」*「欲轉換進位數」】，一直乘到小數為 0，再依序「由上往下」取出整數。

Ans: 1) 1001001 2) 111110.01

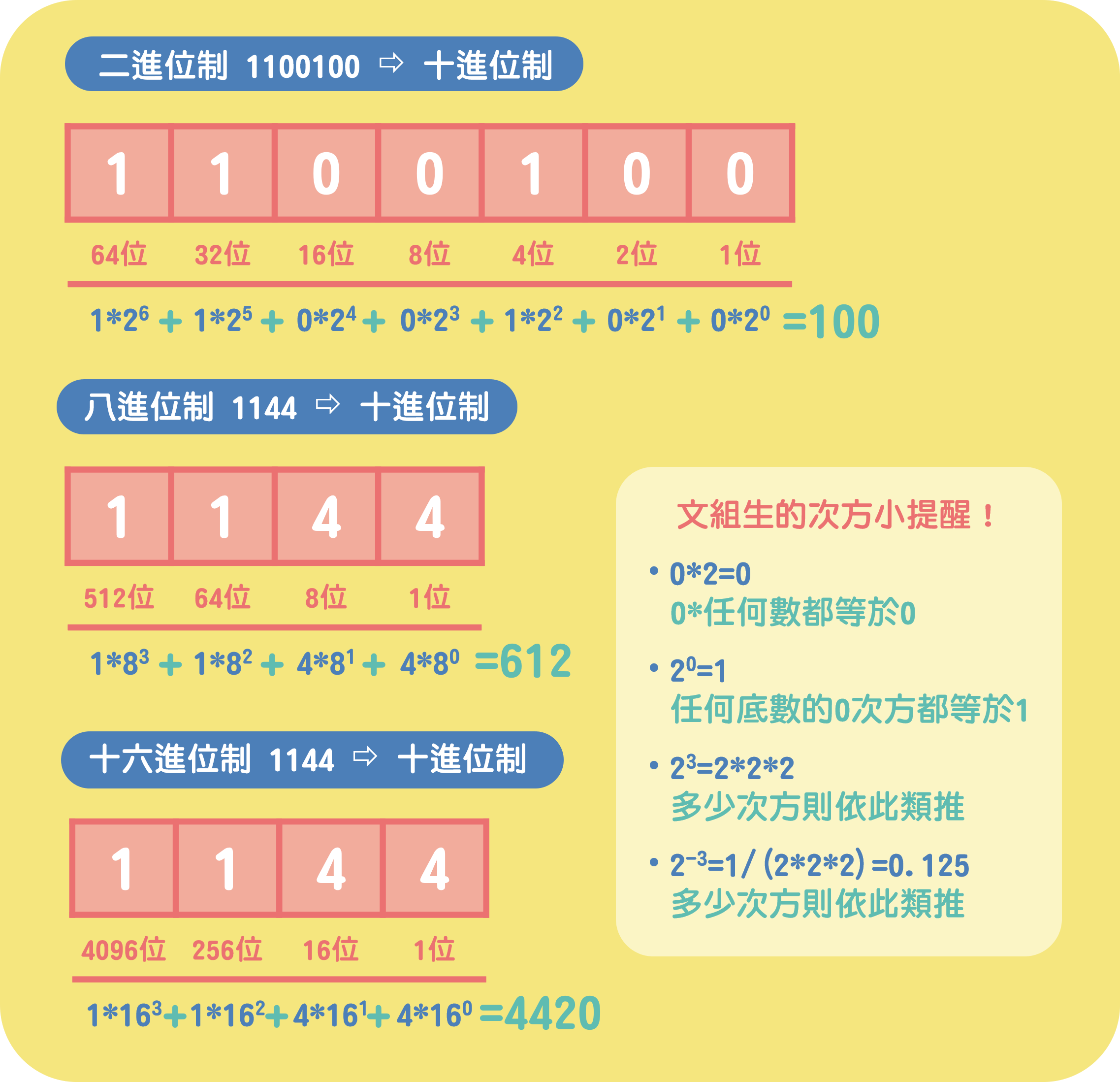
其他進位制轉換為十進位制

二進位制轉換為十六進位制

16為2的四次方，所以二進位制的每4個位數會被分為一組！

  • 以小數點為基準，分向左（整數）右（小數）兩邊，4 個位數為一組

  • 「整數」不足 4 個位數則「前面」補 0

  • 「小數」不足 4 個位數則「後面」補 0

十六進位制轉換二進位制

將十六進位的一個位數以二進位制的4個位數表示，若不足4個位數則「前面」補0

小結

　　看到這邊你一定了解各進位制及轉換的原理了吧！在最後想推薦給大家一個偷吃步網站：CONVERTWORLD.COM，你可以直接輸入數字並挑選想轉換的進位制，是不是很方便呢！

Previous第二章－1111 + 1 ≠ 1112Next2.2 電腦世界的運算 - 1 跟 0 的邏輯運算

Last updated